懺悔錄英文版,哈佛大學板......
And yet (as Thy handmaid told me her son) there had crept upon her a love of wine. For when (as the manner was) she, as though a sober maiden, was bidden by her parents to draw wine out of the hogshead, holding the vessel under the opening, before she poured the wine into the flagon, she sipped a little with the tip of her lips; for more her instinctive feelings refused. For this she did, not out of any desire of drink, but out of the exuberance of youth, whereby, it boils over in mirthful freaks, which in youthful spirits are wont to be kept under by the gravity of their elders. And thus by adding to that little, daily littles (for whoso despiseth little things shall fall by little and little 35) she had fallen into such a habit as greedily to drink off her little cup brim-full almost of wine. Where was then that discreet old woman, and that her earnest countermanding? Would aught avail against a secret disease, if Thy healing hand, O Lord, watched not over us? Father, mother, and governors absent, Thou present, who createdst, who callest, who also by those set over us, workest something towards the salvation of our souls, what didst Thou then, O my God? how didst Thou cure her? how heal her? didst Thou not out of another soul bring forth a hard and a sharp taunt, like a lancet out of Thy secret store, and with one touch remove all that foul stuff? For a maid-servant with whom she used to go to the cellar, falling to words (as it happens) with her little mistress, when alone with her, taunted her with this fault, with most bitter insult, calling her wine-bibber. With which taunt, she, stung to the quick, saw the foulness of her fault, and instantly condemned and forsook it. As flattering friends pervert, so reproachful enemies mostly correct. Yet not what by them Thou doest, but what themselves purposed, dost Thou repay them. For she in her anger sought to vex her young mistress, not to amend her; and did it in private, for that the time and place of the quarrel so found them; or lest herself also should have anger, for discovering it thus late. But Thou, Lord, Governor of all in heaven and earth, who turnest to Thy purposes the deepest currents, and the ruled turbulence of the tide of times, didst by the very unhealthiness of one soul heal another; lest any, when he observes this, should ascribe it to his own power, even when another, whom he wished to be reformed, is reformed through words of his.
教育輸贏
Sony CASE
校園午餐:午餐自行解決:素食50;買錢新祖思想與文化論集;焦竑與晚明新儒思想的重構
晚上楊澤泉兄來訪,他是很難溝通的人---在校長選舉制等;他在推銷雇用流浪教師(博士畢)當學長寢室之專職輔導人(學校提供宿舍,月薪4萬多採募款.....),這是典型的有錘子找釘子的故事。他9點多走,雨勢大.......
花些時間寫翻譯檢討:
錢新祖三書《 中國思想史講義 》《思想與文化論集》《焦竑與晚明新儒思想的重構》
- 「思想,重慶南路」特展,重慶南路一段書店街, 1961 元旦;1973年《ECHO》(英文漢聲)12...
- 懷舊霓虹,香港尋找自我身份的隱喻 Hong Kong’s Storied Neon Signs G...
- 台北中華路1961
- 台北地圖:1968年國民小學《社會》課本
- 案,撫,撥弄,撫客,案甲,年頭,案牘,撥弄是非,搬弄是非
- 滋,汦 , 滋擾,燒酒,私燒,有滋有味
- 自,柊,自生自滅
- 口,嗆,氣急, 火種,在室男、在室女,氣急敗壞
- 繫,繫著, 收束, 文字,約束,束身
故宮展ポスター、修正に乗り出す 台湾の抗議受け
- 2014/6/23 1:42
【台北=共同】東京国立博物館で24日から開催予定の「故宮展」のポスターなどから、正式名称にある「国立」の文字が削除されているとして台湾側が抗議している問題で、日本側は22日までに、台湾の要請に応じて修正に乗り出した。一通り作業を終えて台湾側の承認を得た上で、予定通り23日に開幕式を開き、開催を迎えたい考え。
東博によると、東京都内の駅などに掲示されている「国立」の文言のないポスターに紙を貼るなどして修正作業を23日未明までに終える予定。文言のない前売り券の販売中止も販売会社に指示した。作業終了時点で台湾側に連絡、開催の同意を得る意向だ。
台湾側は20日の総統府の抗議声明で文言修正に応じなければ故宮展中止もあり得るとしていたが、21日の故宮声明では「日本側の対応を見た上で開催に同意するか決める」と態度をやや軟化。
故宮博物院は22日、予定していた馬英九総統夫人の周美青氏の開幕式出席を見送ると発表。馮明珠院長の出席は日本側の修正作業を見極めた上で決めるとしている。
The Great Russian Piano Tradition
Airs Thursdays at 8 pm and Sundays at 10 pm on WQXR.
Russia has given the classical world many gifts, but perhaps the greatest is an unrivaled repertoire for the piano. The music is romantic, demanding and suffused with the passion of the Slavic soul.
The Great Russian Piano Tradition is a new series dedicated to Russian composers and performers. Over the course of 13 weeks, scholar David Dubal traces the history of piano music in Russia and captures the larger-than-life characters who have brought it to life.
Dubal presents carefully curated programs on Pyotr Ilyich Tchaikovsky, Sergei Rachmaninoff and Sergei Prokofiev as well as lesser-known composers such as Nikolai Medtner, Sergei Taneyev and Sergei Lyapunov. You’ll hear a range of soloists, with a special focus on the undisputed giants of the instrument: Vladimir Horowitz, Sviatoslav Richter and Emil Gilels.
Without Shannon's information theory there would have been no internet
It showed how to make communications faster and take up less space on a hard disk, making the internet possible
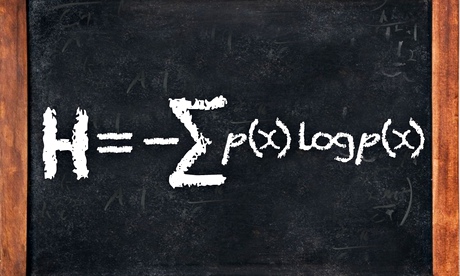
Shannon’s information theory
This equation was published in the 1949 book The Mathematical Theory of Communication, co-written by Claude Shannon and Warren Weaver. An elegant way to work out how efficient a code could be, it turned "information" from a vague word related to how much someone knew about something into a precise mathematical unit that could be measured, manipulated and transmitted. It was the start of the science of "information theory", a set of ideas that has allowed us to build the internet, digital computers and telecommunications systems. When anyone talks about the information revolution of the last few decades, it is Shannon's idea of information that they are talking about.
Claude Shannon was a mathematician and electronic engineer working at Bell Labs in the US in the middle of the 20th century. His workplace was the celebrated research and development arm of the Bell Telephone Company, the US's main provider of telephone services until the 1980s when it was broken up because of its monopolistic position. During the second world war, Shannon worked on codes and methods of sending messages efficiently and securely over long distances, ideas that became the seeds for his information theory.
Before information theory, remote communication was done using analogue signals. Sending a message involved turning it into varying pulses of voltage along a wire, which could be measured at the other end and interpreted back into words. This is generally fine for short distances but, if you want to send something across an ocean, it becomes unusable. Every metre that an analogue electrical signal travels along a wire, it gets weaker and suffers more from random fluctuations, known as noise, in the materials around it. You could boost the signal at the outset, of course, but this will have the unwanted effect of also boosting the noise.
Information theory helped to get over this problem. In it, Shannon defined the units of information, the smallest possible chunks that cannot be divided any further, into what he called "bits" (short for binary digit), strings of which can be used to encode any message. The most widely used digital code in modern electronics is based around bits that can each have only one of two values: 0 or 1.
This simple idea immediately improves the quality of communications. Convert your message, letter by letter, into a code made from 0s and 1s, then send this long string of digits down a wire – every 0 represented by a brief low-voltage signal and every 1 represented by a brief burst of high voltage. These signals will, of course, suffer from the same problems as an analogue signal, namely weakening and noise. But the digital signal has an advantage: the 0s and 1s are such obviously different states that, even after deterioration, their original state can be reconstructed far down the wire. An additional way to keep the digital message clean is to read it, using electronic devices, at intervals along its route and resend a clean repeat.
Shannon showed the true power of these bits, however, by putting them into a mathematical framework. His equation defines a quantity, H, which is known as Shannon entropy and can be thought of as a measure of the information in a message, measured in bits.
In a message, the probability of a particular symbol (represented by "x") turning up is denoted by p(x). The right hand side of the equation above sums up the probabilities of the full range of symbols that might turn up in a message, weighted by the number of bits needed to represent that value of x, a term given by logp(x). (A logarithm is the reverse process of raising something to a power – we say that the logarithm of 1000 to base 10 – written log10(1000) – is 3, because 103=1000.)
A coin toss, for example, has two possible outcomes (or symbols) – x could be heads or tails. Each outcome has a 50% probability of occurring and, in this instance, p(heads) and p(tails) are each ½. Shannon's theory uses base 2 for its logarithms and log2(½) is -1. That gives us a total information content in flipping a coin, a value for H, of 1 bit. Once a coin toss has been completed, we have gained one bit of information or, rather, reduced our uncertainty by one bit.
A single character taken from an alphabet of 27 has around 4.76 bits of information – in other words log2(1/27) – because each character either is or is not a particular letter of that alphabet. Because there are 27 of these binary possibilities, the probability of each is 1/27. This is a basic description of a basic English alphabet (26 characters and a space), if each character was equally likely to turn up in a message. By this calculation, messages in English need bandwidth for storage or transmission equal to the number of characters multiplied by 4.76.
But we know that, in English, each character does not appear equally. A "u" usually follows a "q" and "e" is more common than "z". Take these statistical details into account and it is possible to reduce the H value for English characters to less than one bit. Which is useful if you want to speed up comms or take up less space on a hard disk.
Information theory was created to find practical ways to make better, more efficient codes and find the limits on how fast computers could process digital signals. Every piece of digital information is the result of codes that have been examined and improved using Shannon's equation. It has provided the mathematical underpinning for increased data storage and compression – Zip files, MP3s and JPGs could not exist without it. And none of those high-definition videos online would have been possible without Shannon's mathematics.


沒有留言:
張貼留言